Den Mythos zerstreuen

Zunächst kann das typische HF-SWR-Messgerät die Vorwärts- und Rückwärtsleistung, Spannung oder den Strom nicht separat abtasten. Jede Beschreibung des Geräts oder seiner Schaltung, die auf diese Fähigkeit hinweist, ist fehlerhaft. Wir können dies empirisch mit zwei verschiedenen Experimenten zeigen.

Experiment 1

Schließen Sie einen 100-Ohm-Widerstand direkt an den Ausgang eines 50-Ohm-SWR-Messgeräts (kein Koaxialkabel) an und schließen Sie das direkt an Eingang des SWR-Messgeräts zum Sender (kein Koaxialkabel). Der Widerstand leitet die gesamte Leistung ab, die der Sender in die 100-Ohm-Last abgeben kann - keine Reflexionen von Spannung, Strom oder Leistung, da keine Übertragungsleitung vorhanden ist. Das Messgerät zeigt jedoch ein 2: 1-SWR an.

Experiment 2

Schließen Sie den Sender direkt an den Eingang des 50-Ohm-SWR-Messgeräts an. Schließen Sie am Ausgang des SWR-Messgeräts ein 75-Ohm-Koaxialkabel an und schließen Sie eine 75-Ohm-Last an dessen Ende an. Da die Last mit dem Zo (charakteristische Impedanz) des Koaxialkabels übereinstimmt, gibt es keine Reflexionen von Spannung, Strom oder Leistung am Koaxialkabel. Das Messgerät zeigt jedoch ein SWR von 1,5: 1.

Wie funktioniert es?

Das typische HF-SWR-Messgerät arbeitet durch Abtasten der komplexen Spannung und Strom an dem Einfügepunkt, aus dem das effektive SWR am Einfügepunkt auf einer Übertragungsleitung mit einer charakteristischen Impedanz von 50 Ohm (oder einer Impedanz, für die das SWR-Messgerät ausgelegt ist) berechnet wird.

Der Begriff "effektiv" wird hier verwendet, da die Berechnung unabhängig davon durchgeführt wird, ob eine Übertragungsleitung vorhanden ist oder nicht und unabhängig von der tatsächlichen charakteristischen Impedanz einer vorhandenen Übertragungsleitung.

Abtasten der Spannung

SWR-Messgeräte verwenden eine von drei verschiedenen Methoden, um die komplexe Spannung am Einfügepunkt abzutasten.

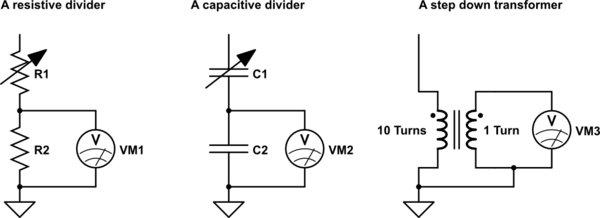
^{simulieren diese Schaltung - Schema erstellt mit CircuitLab sup>}

In jedem Fall senkt die Spannungsabtastschaltung die höhere Spannung, die an der Übertragungsleitung am Einfügepunkt anliegt, auf eine handlichere niedrigere Spannung für die SWR-Messschaltung. Im Fall der resistiven und kapazitiven Teilerschaltungen ist das obere Element typischerweise einstellbar, damit das SWR-Messgerät kalibriert werden kann (dazu später mehr).

Die an der Übertragungsleitung am Punkt von Die Abtastung ist die komplexe Summe aller Durchlassspannungen plus der Summe aller reflektierten Spannungen, die sich aus einer nicht übereinstimmenden Last und Quelle ergeben. Dies kann ausgedrückt werden als:

$$ V_ \ text {line} = V_f + V_r \ tag 1 $$ span>

wobei Vf die komplexe Durchlassspannung und Vr die komplexe reflektierte Spannung am Abtastpunkt ist.

$$ V_1 = (V_f + V_r) * k_1 \ tag 2 $$ span>

wobei k1 die Skalierungskonstante ist, die durch das Design der Spannungsabtastschaltung bestimmt wird.

Abtasten des Stroms

Nahezu jedes SWR-Messgerät verwendet dieselbe Technik, um den komplexen Strom abzutasten, der zum Zeitpunkt des Einfügens auf der Übertragungsleitung vorhanden ist. Die Technik beinhaltet eine Schaltung, die auf den ersten Blick wie ein Aufwärtsspannungstransformator mit einem Lastwiderstand auf der Sekundärseite aussieht, aber tatsächlich eine spezielle Konfiguration ist, die als Breitbandstromtransformator bekannt ist.

Ein Breitband Der Stromwandler wandelt den HF-Strom, der durch seine Primärseite fließt, in eine proportionale HF-Spannung auf der Sekundärseite um. Die Umwandlung erfolgt durch Platzieren eines Lastwiderstands (manchmal als Last bezeichnet) auf der Sekundärseite. Der Lastwiderstand muss viel kleiner als die charakteristische Impedanz der Sekundärseite des Transformators sein, damit diese Strom-Spannungs-Umwandlung proportional ist.

^{simulieren Sie diese Schaltung sup>}

Der Transformator ist typischerweise eine Toroidvorrichtung, bei der der Mittelleiter der Übertragungsleitung durch das Loch des Toroids verläuft, um eine 1-Windungs-Primärwicklung zu bilden, wobei die Sekundärwicklung mehrmals durch die Toroidform gewickelt ist.

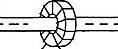
Der komplexe Strom, der zum Zeitpunkt der Abtastung auf der Übertragungsleitung vorhanden ist, ist die Differenz zwischen dem Durchlassstrom und dem reflektierten Strom:

$$ I_ \ text {line} = I_f-I_r \ tag 3 $$ span>

wobei I _{f sub> ist der komplexe Durchlassstrom und I r sub> ist der komplexe reflektierte Strom.}

Die komplexe Spannung, die sich aus dem abgetasteten Strom unter Verwendung eines Breitbandstromwandlers ergibt, kann dann ausgedrückt werden als:

$$ V_2 = (I_f -I_r) * k_2 \ tag 4 $$ span>

wobei k _{2 sub> der Transformationsfaktor in Volt / Ampere ist, der durch die Breitbandstromwandlerschaltung bestimmt wird Design.}

Berechnung des SWR und der Leistung

Wir brauchen jetzt eine Möglichkeit, die abgetastete Spannung und den abgetasteten Strom zur Berechnung des SWR sowie des Vorwärts- und des reflektierten Werts zu verwenden Leistung. Die meisten Gleichungen zur Berechnung dieser Werte beinhalten die Kenntnis der Durchlassspannung und der reflektierten Spannung. Bisher haben wir jedoch nur V1, das proportional zur Summe dieser komplexen Spannungen ist, wie in Gleichung 2 gezeigt. Es gibt jedoch eine andere Möglichkeit, den am Abtastpunkt vorhandenen komplexen Strom auszudrücken das kann uns helfen:

$$ I_ \ text {line} = \ frac {V_f-V_r} {Z_o} \ tag 5 $$ span>

wobei Z _{o sub> die charakteristische Impedanz der Übertragungsleitung ist, typischerweise 50 Ohm in Amateurfunkanwendungen.}

Wir können dann Gleichung 5 in Gleichung 4 einsetzen :

$$ V_2 = (V_f-V_r) * \ frac {k_2} {Z_o} \ tag 6 $$ span>

Nun subtrahieren wir V 2 in Gleichung 6 von V 1 in Gleichung 2:

$$ V_1-V_2 = \ Bigl ((V_f + V_r) * k_1 \ Bigr) - \ Bigl ((V_f-V_r) * \ frac {k_2} {Z_o} \ Bigr) \ tag 7 $$ span>

Mit einem Z _{o sub> von 50 Ohm, wenn wir k 2 sub> auf k 1 sub> -Verhältnis zu 50, Gleichung 7 ist stark vereinfacht:}

_{[Bearbeiten: Die Formeln 8 und 9 wurden aktualisiert] sub> sub> sub>}

$$ V_1-V_2 = ((V_f + V_r) - (V_f-V_r)) * k_1 = V_r * 2 * k_1 \ tag 8 $$ span>

Beibehaltung des gleichen Verhältnisses von k _{2 sub> zu k 1 sub>, aber Hinzufügen von V 1 sub> und V 2 sub>:}

$$ V_1 + V_2 = ((V_f + V_r) + (V_f-V_r)) * k_1 = V_f * 2 * k_1 \ tag 9 $$ span>

Da der Term 2 * k _{1 sub> eine dem Designer bekannte Konstante ist, kann er im Folgenden leicht herausgerechnet werden Anwendungen der Gleichungen 8 und 9.}

Dieses Addieren und Subtrahieren von V1 und V2 wurde in der Vergangenheit mit einem Schalter am SWR erreicht Meter. Nun ist es üblicher, dass V1 in einen Mittelabgriff der Sekundärseite des Breitbandstromtransformators eingespeist wird. Mit den geeigneten Schaltungswerten ist ein Zweig des Transformators dann V1 + V2, während der andere Zweig V -V ist > 2 sub>.

Da die Leistung proportional zur quadratischen Spannung ist, gibt Gleichung 8 eine Spannung an, die proportional zur reflektierten Leistung ist, während Gleichung 9 eine Spannung liefert, die proportional zur Durchlassleistung ist. Jede dieser Spannungen wird ihrer jeweiligen Zählerbewegung zugeführt, wobei die auf der Zählerfläche gezeichnete logarithmische Skala die Umwandlung der linearen Zählerauslenkung, die auf der Spannung basiert, in Leistung umwandelt.

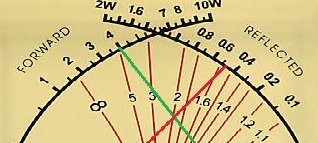
Die Umwandlung von Vorwärtsleistung und reflektierter Leistung in SWR wird wie folgt angegeben:

$$ SWR = \ frac { 1+ \ sqrt {\ frac {P_r} {P_f}}} {1- \ sqrt {\ frac {P_r} {P_f}}} \ tag {10} $$ span>

Or. En alternativ wird die Umwandlung von Vf und Vr in SWR wie folgt angegeben:

$$ SWR = \ frac {1+ (V_r / V_f)} {1- (V_r / V_f)} \ tag {11} $$ span>

Die oben abgebildete Messfläche zeigt den Schnittpunkt der beiden Nadeln auf der 2: 1-SWR-Linie, der für die gezeigten Leistungen der Gleichung 10 entspricht. Der SWR-Zählerdesigner zeichnet einfach eine Anzahl von SWR-Werten auf dem Zähler auf, die dem Schnittpunkt der Vorwärts- und der reflektierten Leistung entsprechen.

Kalibrieren des SWR-Zählers

Die typische Kalibrierungsroutine für das SWR-Messgerät besteht darin, eine Widerstandslast, die gleich dem Z o der Zuleitung ist, direkt an den Ausgang des Messgeräts anzubringen. Ein Sender gibt die entsprechende Leistung an den Eingang des SWR-Messgeräts aus. Das Spannungsteilungsnetzwerk wird dann so eingestellt, dass P r gleich 0 ist. Da P r proportional zu (V r ) ^{2 sup> können wir aus Gleichung 7 sehen, dass diese Anpassung einfach sicherstellt, dass k _{2 sub> / k 1 sub> = 50 für ein SWR ist Messgerät, das für eine 50-Ohm-Zuleitung ausgelegt ist.}}